Clay brick vs concrete block retaining walls – What is the structural difference?

Summary

Mass masonry gravity retaining walls are commonly used to form retaining structures within residential developments for retained heights up to circa 2m. They were a very common form of retaining structure in history.

In the modern construction environment, the cost of laying concrete block in place of clay brick is less. Since other than the face, the structure of the retaining wall is not visible, it is only natural to ask whether it makes a structural difference to the thickness of the stem and therefore the amount of masonry required to construct the wall.

The short answer is yes, it does make a difference. Concrete block is weaker than clay brickwork when building retaining walls and a stem constructed from concrete block can expect to be circa 50% thicker than its clay brick counterpart if the declared compressive strength fo the block is $\leq$ 7.3MPa. This technical note explains why and presents the structural analysis in justification.

This note may be of use to those assessing the financial viability of retaining structures. It will facilitate informed judgement on whether the reduced cost of supply and laying of the block balances the increase in masonry volume required for equivalent strength.

What makes the stem stand up

The stem of a mass masonry retaining wall has to resist shear forces and bending moments to stand up. These force effects are applied by the retained soil and the surcharge. Both the bending strength and the shear strength of masonry are enhanced by the weight of the stem, the basic strength of the masonry and the thickness of the stem.

The basic strength of masonry

The basic strength of masonry is presented in the National Annex to BS EN 1996-1-1. Shear strength $f_{vko}$ and bending strength $f_{xk1}$ for M4 to M6 mortar are indicated in the table below. This table assumes that the block has a declared compressive strength $\leq$ 7MPa.

Masonry type	$f_{vko}$ (MPa)	$f_{xk1}$ (MPa)
Clay	0.20	0.40
Block (aggregate)	0.15	0.15

These basic values show that aggregate block is 25% weaker than clay brick in shear and 62% weaker in bending before accounting for self-weight.

For typical mass masonry retaining walls in developments bending strength is the governing factor in the design of the stem. Therefore, to simplify the comparison, only bending strength will be considered below.

Self weight of the stem

Medium-density aggregate concrete blocks have a density $\gamma_d$ of circa $1500 kg/m^3$ whilst clay brick is circa $2000 kg/m^3$ . Hence clay brickwork is circa 33% denser than medium dense aggregate block.

The bending strength of the stem is given by:

$\frac{f_{xk1}}{\gamma_M} + g_d$

Where $g_d = \gamma_d h$ with $\gamma_M$ being the partial factor (of safety) applied to the masonry and $\gamma_d$ being the density of the masonry and $h$ being the height of the stem above the level at which the strength is considered.

A comparison of bending strength over the height of the stem

Assuming the above parameters and that $\gamma_M = 2.7$ the following plot shows the difference in bending strength of concrete aggregate block and clay brick masonry.

Hence, aggregate concrete block has a significantly weaker bending strength when compared to clay brick.

The effect of stem thicknes

So far in the above calculations, the stem thickness has not been a factor. The stem thickness comes into play when calculating the bending capacity of the stem. The above is just the strength of the masonry itself. The bending capacity of the stem is given by:

$Z(\frac{f_{xk1}}{\gamma_M} + g_d)$

Where Z is a geometric property called the section modulus and is given by $Z = b t^2 / 6$ . The length of the wall $b$ is taken to be 1000mm and $t$ is the thickness of the wall. The bending capacity of the stem is therefore given by:

$\frac{bt^2}{6}(\frac{f_{xk1}}{\gamma_M} + g_d)$

The effect of the section modulus is to amend the linear relationship of strength and introduce a parabolic relationship for stem capacity in terms of its thickness.

A comparison of stem bending capacity

From the above, it is possible to establish a ratio between block and brick thickness over the height of the stem to give the equivalent bending capacity.

$\frac{bt_{block}^2}{6} (\frac{f_{xkblock}}{\gamma_M} + \gamma_{dblock} h) = \frac{bt_{brick}^2}{6} (\frac{f_{xkbrick}}{\gamma_M} + \gamma_{dbrick} h)$

Which transposes to:

$\frac{t_{block}}{t_{brick}} = \sqrt{\frac{(\frac{f_{xkbrick}}{\gamma_M} + \gamma_{dbrick} h)}{(\frac{f_{xkblock}}{\gamma_M} + \gamma_{dblock} h)}}$

This ratio is plotted in the graph below:

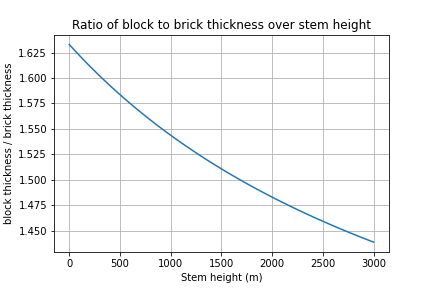
This graph indicates that a stem made from block can expect to be circa 50% thicker than the equivalent clay brick stem based on bending strength. Note, that if the delcared compressive strength of the block is $\geq$ 10.5MPa then this increase in thickness may decrease to circa 25%.

Conclusion

Mass masonry retaining wall stems construction from concrete aggregate blockwork can expect to be 50% thicker than their clay brick counterparts for block with a declared compressive strength of $\leq$ 7.3MPa. For some walls, this will also impact on foundation width. This provides a guide for cost consultants and quantity surveys to assess comparable costs when optimising mass masonry retaining walls for a development.

The compatibility considerations of applying a clay facing brick leaf to the front of an aggregate concrete block mass masonry retaining wall are not considered in this note.